
grand dodécicosidodécaèdre ditrigonal

grand icosicosidodécaèdre

grand dodécicosaèdre
mêmes sommets et arêtes que les deux autres !
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
GRAND DODÉCICOSIDODÉCAÈDRE DITRIGONAL,
GRAND ICOSICOSIDODÉCAÈDRE et GRAND DODÉCICOSAÈDRE
Great ditrigonal dodecicosidodecahedron, great icosicosidodecahedron
and great dodecicosahedron,
Großes Dodekikosidodecaeder, großes Ikosikosidodekaeder
und großes Dodekikosaeder

grand dodécicosidodécaèdre ditrigonal |

grand icosicosidodécaèdre |

grand dodécicosaèdre |
|
| Famille | polyèdre étoilé semi-régulier (ou uniforme U42), ou polyèdre de Badoureau | idem U48 | idem U63 |
| Étymologie | dodec car il a 12 faces pentagonales, icosi car il a 20 faces triangulaires et dodeca car il y a 12 faces décagonales ; ditrigonal car ?? et grand pour le différencier du petit | icos car il a 20 faces triangulaires, icosi car il y a 20 faces hexagonales et dodeca car il y a 12 faces pentagonales ; grand pour le différencier du petit | dodec car il a 12 faces decagonales, icosa car il a 20 faces hexagonales ; grand pour le différencier du petit |
| Dual | |||
| faces | 20 triangles, 12 pentagones et 12 décagones étoilés | 20 triangles, 12 pentagones et 20 hexagones | 20 hexagones et 12 décagones étoilés |
| Sommets | 60 sommets , de code de Schläfli 3.10/3.5.10/3 | 60 sommets, de code de Schläfli 5.6.3.6 | 60 sommets, de code de Schläfli (6.10/3)2 |
| Arêtes | 120 arêtes | idem | idem |
| Construction | les sommets sont ceux du dodécaèdre tronqué | idem
mêmes sommets et arêtes que les deux autres ! |
idem |
| Groupe des isométries | celui de l'octaèdre | idem | idem |
Les faces triangulaires, pentagonales, hexagonales et décagonales
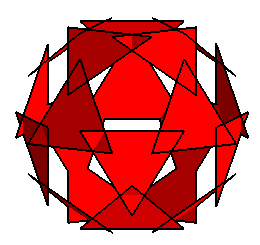 |
 |
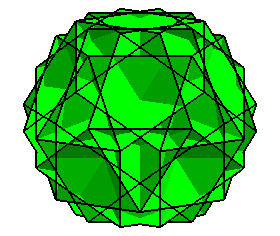 |
 |
Ces trois polyèdres sont à la symétrie
dodécaédrique ce que sont ceux-ci
à la symétrie cubique.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2008